Czy to oznacza, że prognozy pogody będą teraz 1000 razy dokładniejsze?!? 
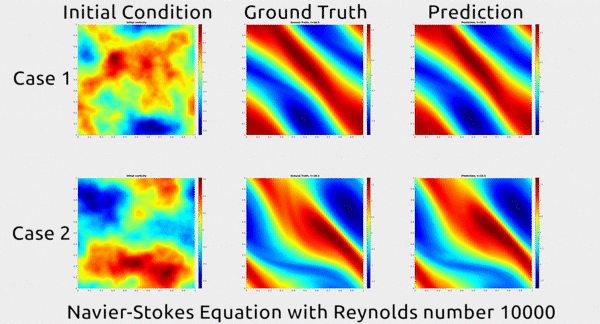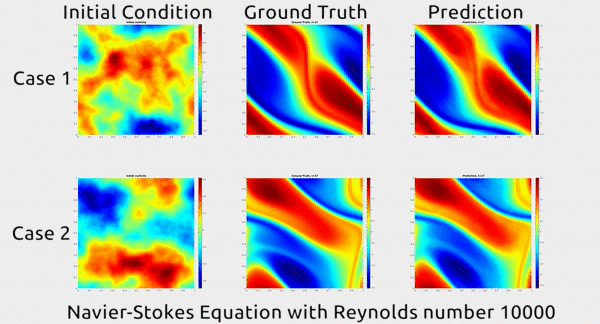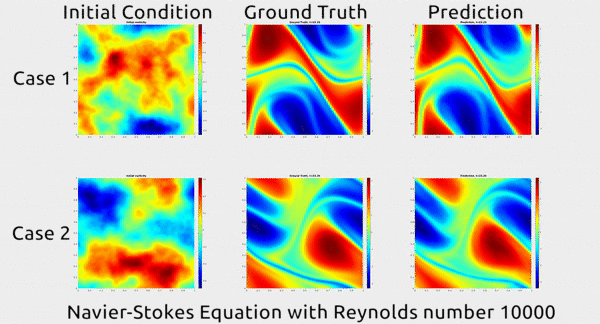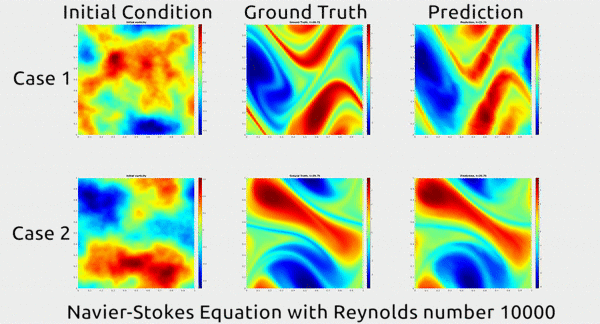
GT:
https://translate.google.com/translate?hl=en&sl=en&tl=pl&u=https%3A%2F%2Fwww.technologyreview.com%2F2020%2F10%2F30%2F1011435%2Fai-fourier-neural-network-cracks-navier-stokes-and-partial-differential-equations%2F&sandbox=1
Badania:
https://arxiv.org/abs/2010.08895
#nauka #matematyka #informatyka #ai

These calculations (PDE) are highly complex and computationally intensive, which is why disciplines that use a lot of PDEs often rely on supercomputers to do the math. It’s also why the AI field has taken a special interest in these equations. If we could use deep learning to speed up the process of solving them, it could do a whole lot of good for scientific inquiry and engineering.
Now researchers at Caltech have introduced a new deep-learning technique for solving PDEs that is dramatically more accurate than deep-learning methods developed previously. It’s also much more generalizable, capable of solving entire families of PDEs—such as the Navier-Stokes equation for any type of fluid—without needing retraining. Finally, it is 1,000 times faster than traditional mathematical formulas, which would ease our reliance on supercomputers and increase our computational capacity to model even bigger problems. That’s right. Bring it on.

GT:
https://translate.google.com/translate?hl=en&sl=en&tl=pl&u=https%3A%2F%2Fwww.technologyreview.com%2F2020%2F10%2F30%2F1011435%2Fai-fourier-neural-network-cracks-navier-stokes-and-partial-differential-equations%2F&sandbox=1
Badania:
https://arxiv.org/abs/2010.08895
#nauka #matematyka #informatyka #ai


Brak komentarzy. Napisz pierwszy